Frequency sweep and dispersive materials

This example show how to make frequency sweeps and hot to treat dispersive materials in a simulation.

Import packages

import numpy as np
import matplotlib.pyplot as plt

import remsol
from remsol import Polarization as pol

Frequency sweep

Structure definition

Structure definition is the same as in the previous example.

# Define the layers
layers = [
    remsol.Layer(n=1.0, d=1.0),
    remsol.Layer(n=2.0, d=1.0),
    remsol.Layer(n=1.0, d=1.0),
]

# Define the multilayer
multilayer = remsol.MultiLayer(layers)

Wrapper function definition

Instead of calling multilayer.neff directly, we will define a wrapper function which catches the exception and returns np.nan in case the mode is not found.

def neff_wrapper(omega: float, polarization: pol, mode: int):
    try:
        return multilayer.neff(omega, polarization, mode)
    except Exception as e:
        return np.nan

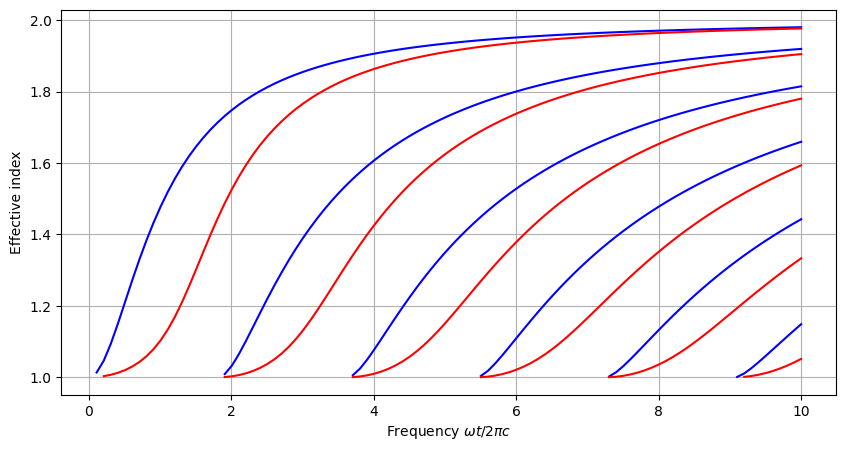
omegas = np.linspace(0.01, 10, 101)
fig, ax = plt.subplots(1,1, figsize=(10, 5))
for mode in range(8):
    neffs = [neff_wrapper(om, pol.TE, mode) for om in omegas]
    ax.plot(omegas, neffs, 'b-')
    neffs = [neff_wrapper(om, pol.TM, mode) for om in omegas]
    ax.plot(omegas, neffs, 'r-')
ax.set_xlabel('Frequency $\omega t/2 \pi c$')
ax.set_ylabel('Effective index')
ax.grid()

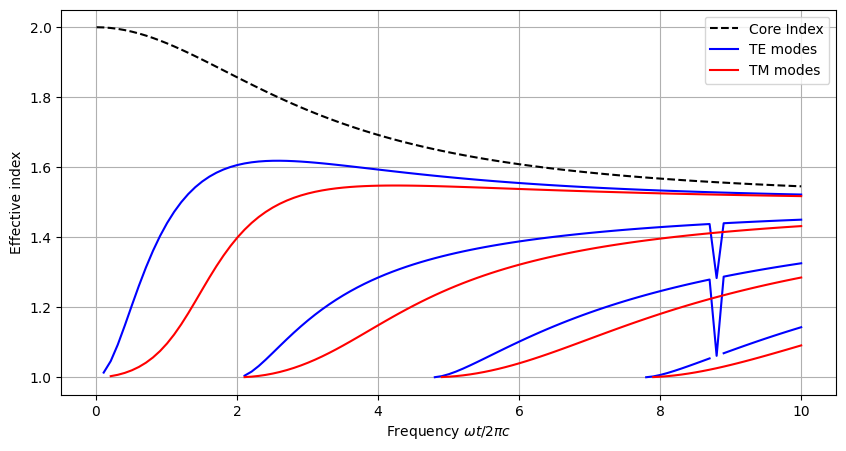
Dispersive materials

The module has no built-in support for dispersive materials, but it is possible to define the structure as a function of frequency and call the solver for each frequency.

Wrapper function defiition

It is still important for the wrapper function to handle the mode not found exception.

def n_function(omega: float):
    return 2.0 -0.5 * omega**2 / (10.0+omega**2)


def calculate_neff(omega: float, polarization: pol, mode: int):
    layers = [
        remsol.Layer(n=1.0, d=1.0),
        remsol.Layer(n=n_function(omega=omega), d=1.0),
        remsol.Layer(n=1.0, d=1.0),
    ]
    
    multilayer = remsol.MultiLayer(layers)
    
    try:
        return multilayer.neff(omega, polarization, mode)
    except Exception as e:
        return np.nan
    
omegas = np.linspace(0.01, 10, 101)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for mode in range(8):
    neffs = [calculate_neff(om, pol.TE, mode) for om in omegas]
    te_plot=ax.plot(omegas, neffs, "b-")
    neffs = [calculate_neff(om, pol.TM, mode) for om in omegas]
    tm_plot=ax.plot(omegas, neffs, "r-")
core_plot = ax.plot(omegas, [n_function(omega=om) for om in omegas], "k--")
ax.legend([core_plot[0], te_plot[0], tm_plot[0]], ["Core Index", "TE modes", "TM modes"], loc="upper right")
ax.set_xlabel("Frequency $\omega t/2 \pi c$")
ax.set_ylabel("Effective index")
ax.grid()